[통계학습개론] Linear Regression
Linear regression
supervised learning, 비교적 간단한 통계 방법, 해석력 ↑
선형성(X,Y 선형관계), 등분산성(추정식 잔차는 등분산), 독립성(추정식 잔차들 독립적), 정규성(정규분포, 잔차 평균=0)을 가정한다.
a linear regression model은
the regression function f(YⅠX) 가 the inputs X1, … ,Xp에 linear하다는 것을 가정한다.
- Model
$f\left(X\right)=\beta _0+\sum _{j=1}^pX_j\ \beta _j$
a set of training data : (x1,y1), … , (xN,yN)
-> 이것으로부터 parameters β 추정가능
각 xi=(xi1,xi2, … , xip)’은 i번째에 대한 특징 측정값의 벡터이다.
- Estimation
가장 유명한 측정 방법 : least squares
-> MSE를 최소화하는, RSS를 최소화하는 β hat, … , βhat을 구한다.
-> RSS 식을 미분해서 0이 되는 지점을 찾는다. (미적분에서 함수의 최솟값 찾는 방법)
-> p value가 작아 유의하다고 나온 변수여도 데이터에 포함하면 중요성이 떨어지는 경우가 있다.
$RSS\left(\beta \right)=\sum {i=1}^N\left(y_i-\beta _0-\sum _{j=1}^px{ij}\ \beta _j\right)^2=\left(y-X\ \beta \right)’\left(y-X\ \beta \right)$
X : N×(p+1) matrix, β=(β0, … ,βp)’, y : the N vector of outputs in the training set
※ RSS=SSE : 잔차(추정 데이터와 실제 데이터의 차)들을 제곱해서 더한 값.
※ RSE=root MSE, TSS = SST, R2=SSR/SST=1-SSE/SST
※ R2↑, SSE↓ 일수록 데이터 변동을 잘 설명한다.
-> least square 방법으로 추정한 회귀선은 unbiased하다. 다시 말해 많은 데이터에 대해 여러번 least square를 하면 추정 선들의 평균선은 실제 관계선과 같아진다. 이것은 β에도 적용되어 추정 회귀계수의 평균은 실제 관계계수와 같아진다.
-> 추정된 y hat, β hat, β hat의 분산을 구하여 평균선이 얼마나 믿을만한지 확인한다.
=>
$\hat{\beta }=\left(X\ ‘\ X\right)^{-1}X\ ‘\ y$
$\hat{y}=X\ \hat{\beta }=X\left(X\ “\ X\right)^{-1}X\ “\ y=H\ y$
X의 columns가 not linearly independent 일 수 있는데, 그러면 X는 not of full rank이다.
그럼 X’X는 singualr 하고 the least squares coefficients β hat은 유일하게 정의되지 않는다.
이런 경우는 Lidge, Lasso 등의 다른 방법으로 추정해야 한다.
- Inference
다음에 정리
- The Gauss-Markov Theorem(?)
$MSE\left(\hat{\theta }\right)=E\left(\hat{\theta }-\theta \right)^2=Var\left(\hat{\theta }\right)+\left[E\left(\hat{\theta }\right)-\theta \right]^2$
MSE가 작을수록 더 좋은 추정이므로 더 좋은 추정량을 찾을 때 MSE를 사용한다. 위의 식을 보면 MSE는 variance와 squared bias에 영향을 받는다.
β의 the least squares estimates는 모든 linear unbiased estimates 중에서 가장 작은 variance를 갖는다. MSE가 작은 biased estimates는 variance의 감소를 위해 약간의 squared bias의 증가를 감수할 것이라는 것을 주목해야 한다. 어떤 방법이든 the least squares coefficients 중 일부를 축소하거나 0으로 설정하면 biased estimates가 발생할 수 있다.
-> variable selection, ridge regression
The comparison of Linear regression with KNN
- KNN regression
non-parametric method,
$\hat{f}\left(x_0\right)=\frac{1}{K}\sum _{x_i\in N_0}^{ }y_i$
N0 : K training observations, K : fixed coefficient
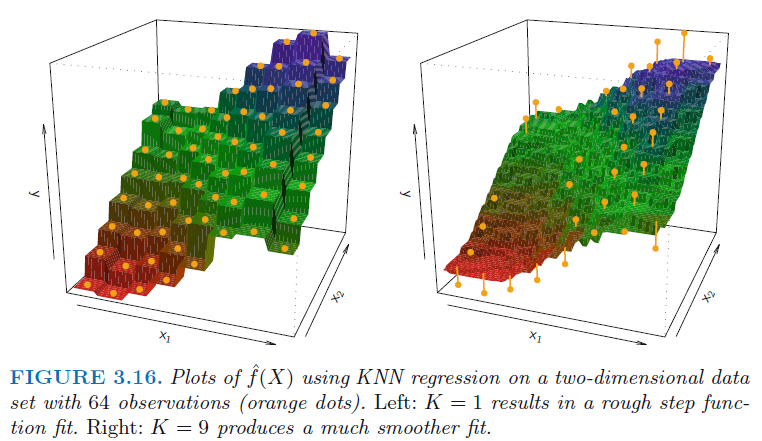
Left : k=1, flexibility ↑, high var ↑, low bias ↓
Right : k=9, flexibility ↓, low var ↓, high bias ↑
적절한 K는 bias variance trase off에 따라 달라진다.
- 차원의 저주(Cur of dimensionality in KNN)
p=1, Y변수까지 2차원일 때는 neighbor을 보고 판단 가능하지만 p=20, 21차원이면 판단할 만한 충분히 비슷한 neighbor이 없다. 즉 고차원이 되면 KNN의 정확도를 감소시킨다.
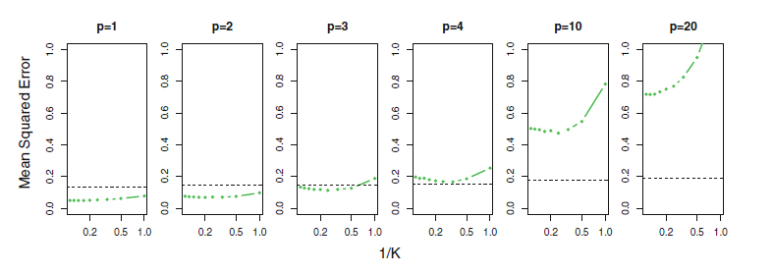
grey : linear regression MSE, green : KNN regression MSE
차원이 작을 때는 KNN이 좋은 분석이지만,
차원이 커질수록 linear regression의 MSE는 변화가 없고
KNN의 MSE는 급격히 증가하여 성능이 급격히 떨어진다.